Regulation of irrigation
canals: characterisation and classification
By Pierre-Olivier Malaterre
These Web Pages are
mainly inspired from the following publication:
Malaterre P.O. 1995.
"Regulation of irrigation canals: characterisation and
classification". International Journal of Irrigation and Drainage Systems,
Vol. 9, n°4, November 1995, p. 297-327.
Other references from
the same author on the same subject:
Malaterre P.O., D.C. Rogers, J. Schuurmans. 1995. "Classification of Canal Control
Systems". First International Conference on Water Resources Engineering,
Irrigation and Drainage, San Antonio, Texas, USA, 14-18 August 1995.
Malaterre P.O. 1995. " La régulation des canaux d'irrigation: caractérisation et classification ", Journal la Houille Blanche, Vol 5/6 - 1995, p. 17-35.
Malaterre P.O. 1994.
"Modelisation, Analysis and LQR Optimal Control of an Irrigation
Canal", PhD Thesis LAAS-CNRS-ENGREF-Cemagref, Etude EEE n°14, ISBN
2-85362-368-8, 220 p.
Malaterre P.O. 1991. "Water Flow Regulation in Irrigation Canals: Present Methods and Perspectives". Workshop at IIMI (International Irrigation Management Institute), Colombo, Sri Lanka, October 1991.
Warning:
The reason why I decided to
start these Web pages is to be able to update easily information on the
Regulation of Irrigation Canals, as soon as I get a new idea or information on
this subject, and to share these materials with everybody in the world, but
without making a new publication every 6 months !
Key words: Automatic, Canal management, Canal
regulation, Classification, Control, Irrigation canal
Abstract. This article suggests and defines a
characterisation of irrigation canal regulation methods, based on four
criteria: considered variables (controlled, measured, and control action
variables), logic of control, design method (structure and technique) and field
implementation (configuration and device). Depending on the chosen criterion
and partition rule, different classifications can be built from this
characterisation. In conclusion, a structured characterisation table of the
main published canal regulation methods is presented.
Abbreviations. ASCE - American Society of
Civil Engineers, CACG - Compagnie d'Aménagement des Coteaux de
Gascogne, CARA - Compagnie d'Aménagement Rural d'Aquitaine, CARDD
- Canal Automation for Rapid Demand Deliveries, CEMAGREF - Centre
National du Machinisme Agricole, du Génie Rural, des Eaux et des
Forêts, CNABRL - Compagnie Nationale d'Aménagement du
Bas-Rhône Languedoc, ELFLO - Electronic Filter and Level Offset, FB
- Feedback or closed-loop control, FBdn - Feedback or closed-loop
downstream control, FBmi - Feedback or closed-loop mixed control, FBup
- Feedback or closed-loop upstream control, FF - Feedforward or
open-loop control, GPC - Generalised Predictive Control, LQR -
Linear Quadratic Regulator, MIMO - Multiple Inputs, Multiple Outputs, nI
mO - n Inputs, m Outputs, P - Perturbation, - Estimation of
perturbations, PID - Proportional, Integral, Derivative Controller, PIR
- Contrôleur Proportionnel, Intégral, Retard (PI Delay
controller), Q - Discharge in the canal, Qdn - Downstream
discharge in the canal, Qin - Intermediate discharge in the canal, Qup
- Upstream discharge in the canal, SCP - Société du Canal
de Provence, SISO - Single Input, Single Output, U - Control
action variable, V - Volume in a canal pool, V - Elementary
control action variable, w - Regulator gate opening, Y -
Controlled variable, Yc - Target controlled variable, y - Water
elevation, ydn - Downstream water elevation of the pool (therefore
upstream of a regulator), yin - Intermediate water elevation in the
pool, yup - Upstream water elevation of the pool (therefore downstream
of a regulator), Z - Measured variable.
INTRODUCTION
Many irrigation canal regulation methods have been developed in the world. These methods differ from a country or region to another. They range from the simplest methods, developed more than 2000 years ago, to the most sophisticated ones developed recently, or under development. The latter use modern automatic control techniques. Numerous articles have been published on the subject. Terminologies employed by the different authors are often confusing. Although various attempts of classification have been made, none are completely satisfactory.
The first section of this article presents the core of the different existing classifications and shows their insufficiencies. Following sections attempt to fulfil this need by defining a characterisation of regulation methods based on four essential criteria. Various classifications can be defined in reference to these four criteria depending on the chosen criterion and partition rule. In conclusion, a table of the characteristics of the various published canal regulation methods is given. Different possible classifications are presented.
This article stems from a PhD Thesis (Malaterre 1994). Its main ideas have been presented at a meeting of the ASCE Task Committee on "Classification of and comparison criteria for automation canal algorithms" on November 4, 1993 at the US Water Conservation Laboratory (Phoenix, Arizona, USA). The purpose of this Task Committee, to which CEMAGREF participates, is to describe and compare the different canal regulation methods existing in the world.
LITERATURE REVIEW
Many authors have attempted to classify the different canal regulation methods developed in the world (Framji et al. 1978, De Leon 1986, Zimbelman 1987, Buyalski et al. 1991, Chevereau 1991, Schuurmans 1991, Malaterre 1991, Deltour 1988 and 1992, Baume et al. 1990 and 1992a, Khaladi 1992, Ankum 1992, 1993a and 1993b, Goussard 1993, Plusquellec et al. 1988 and 1994). Generally, these authors are not control engineers, but irrigation, hydraulic or civil engineers. The concepts they use to differentiate canal regulation methods are from different points of view (e.g.: upstream control and remote control). Furthermore, their definitions are different and sometimes contradictory (e.g.: upstream control by Ankum 1993, Goussard 1993, Chevereau 1991).
Ankum (1993) proposes the following partition rule for his classification: proportional control, upstream control, downstream control, volume control or BIVAL, ELFLO control, and CARDD control. Plusquellec et al. (1994) use a different one: proportional control, adjustable flow-rate control, upstream control, downstream control, remote monitoring, and remote control. These two articles are very representative of the present literature. They are not well structured because the partition rule is not based on distinct concepts, and therefore the resulting classes are not independent. For example, ELFLO and CARDD methods are also downstream control methods (Ankum 1993), and the Dynamic Regulation of SCP is both a remote control and a downstream control method (Plusquellec et al. 1994). These partition rules are only lists of existing methods and field implementation.
Goussard (1993) proposes a better classification of canal regulation methods, based on their implementation configuration: distributed control (upstream, downstream, associated levels, or mixed controls), centralised control (programmed, or real time), and distributed control under centralised control. However, this classification defines upstream and downstream controls as sub-classes of distributed control. And, as noticed by the author himself, these concepts can also be sub-classes of the centralised control. This inaccuracy comes from the fact that his classification is based on two different concepts that should be dissociated: the configuration of field implementation and the logic of control.
Chevereau (1991) underlines the ambiguity of existing classifications. His classification is more satisfactory in the case of a unique pool where the downstream level is controlled by the upstream discharge. In particular, he introduces the essential concept, for the control engineers, of "open-loop" and "closed-loop". However, he links the concept of upstream control with open-loop control (p. 6), and the concept of downstream control with closed-loop control (p. 7). This link only exists in his particular canal regulation example, but not in more general contexts. For example, although GEC Alsthom AMIL gates are the very example of an upstream control, they maintain constant their upstream water level, through a closed-loop.
Nonetheless are these classifications different and not clearly structured, but they are based on misleading terminologies. One major confusion stems from the use of upstream and downstream control terms. Even if downstream control (respectively upstream control) aims traditionally, for technological simplicity, at maintaining a constant water level just downstream (respectively upstream) of the regulator, this is not always the case. This confusion lead to the creation of a new term: "distant downstream control" when the controlled water level is the upstream water level of the next downstream regulator! This new term incorporates two concepts: the controlled variable ("distant") and the logic of control ("downstream control"). To avoid any confusion, these two concepts must be distinguished, and clearly defined. In this paper, controlled water levels are defined in reference to the pool (upstream, middle or downstream level of the pool) and not to the regulator. Furthermore, upstream and downstream controls are defined as logics of control and not in reference to a particular controlled variable.
Ankum (1993) uses the term "self-management" for systems whose command in discharge is achieved by a closed-loop controller. Self-management is not to be confused with self-regulation defined by control engineers (Shinskey 1988). According to Shinskey, a system behaves in self-regulation when it evolves spontaneously to a state of balance. This state of balance is obviously linked to the operating conditions. By opposition, a system behaves in non-self regulation, when it reaches its extreme conditions as soon as the command is not perfectly adjusted to the output objectives. This is the case for a canal feeding pumping stations and whose tailend is closed. When the inflow discharge does not match exactly the total pumped discharge, the canal overtops or dries up. Most irrigation canals function in self-regulation, since excess water is evacuated by the tailend, and emptying is rare since gravity turnouts stop withdrawing water as soon as the main canal water level is too low. So, self-management and self-regulation are very different concepts. Furthermore, self-management does not add anything to the well-known concept of closed-loop. This term "self-management" should be abandoned.
This article presents a classification of the different canal or river regulation methods. Terms used by the irrigation, hydraulic or civil engineers are defined in the more rigorous language of the control engineers. This classification applies to traditional as well as to modern methods. Well-known examples are given to illustrate each concept. Methods are defined through their names, when they do have one, or by the name of their author(s), or by the automatic control theory used. They are not presented in detail. They are abundantly described and studied by their authors or in research or synthesis papers (Zimbelman 1987, Buyalski 1991, Chevereau 1991, Goussard 1993). Precise references are given at the first appearance of each example. They are not repeated thereafter, so as to simplify the perusal of the text.
DEFINITION OF A CLASSIFICATION
In order to classify the elements of a set E, it is necessary to define: (i) a criterion of characterisation, and (ii) a partition rule of the set E based on this criterion. According to Ramis et al. (1979), a "partition" of a set E is mathematically defined as any family of parts of E, non void, separate two by two, and whose gathering restores the set E. Each element of E is then associated to a unique part of the partition. In our case, the considered set E is the set of canal regulation methods either applied or solely theoretically developed.
The difficulty presented by the classification of this set is due to the different ways of characterising its elements (e.g.: controlled variables, configuration of field implementation, communication management, design method, alarm management, length of the considered canal). Among all possible criteria, one wants to retain those, in minimum number, that allow characterisation of the hydraulic behaviour, the performance and the constraints of the various canal regulation methods. We choose to retain the following four essential criteria: considered variables, logic of control, design method, and field implementation. Sub criteria will be defined to refine them.
These different terms are defined, discussed and illustrated in the following sections. The ordering of the four criteria is not linked to any priority of interest. Depending on his technical background, each person may be more or less interested in one or several of the four criteria evoked. Managers and hydraulic engineers are more concerned about controlled variables and the logic of control. Control engineers are more concerned about the logic of control and the design method. Managers and civil engineers are interested in the measured variables and the field implementation.
CONSIDERED VARIABLES
In control theory, a system is usually represented as in Figure 1. U is the system control action variables (e.g.: gate openings, increments of gate opening, discharges), which are acted on, so as to modify the state of the system. Y represents the system controlled variables (e.g.: water levels, discharges, volumes, linear combinations of water levels), to which targets (constant or variable) are assigned.
![]()
Fig. 1.
Controlled variables Y are not always obtained directly from the system, but are sometimes the results of calculations (through a function g) from physical variables Z measured on the system (Figure 2).

Fig. 2.
For example, in the BIVAL method, the controlled variable Y = a yup + (1 - a) ydn, where a ] 0,1 [. Measured variables Z are then upstream (yup) and downstream (ydn) water levels of the pool. A water level can be measured by the motion of a float via a potentiometer, or by a pressure via a piezo-resistive cell, or by the laps time of a wave via an ultrasonic cell. The complex measurement process of these variables Z is not discussed further; However, it is important to know the type, the number and the location of these variables Z.
Similarly, control action variables U cannot always be applied directly to the system. When necessary, they have to be translated, through a function f, into elementary commands V (Figure 2) applicable to the system actuators (e.g.: electrical impulses for an engine, feeding pressure of a hydropneumatic jack). This function f can be split into two functions f1 and f2. f1 transforms the variable U into a gate opening. f2 transforms this gate opening into the variable V. In general, efficient PID controllers with rapid dynamics perform these f2 servo-controls. Therefore, the corresponding dynamics are neglected and the considered elementary commands V are only gate openings. So, it is assumed possible to move a gate into any given position, with an infinite speed and precision (or with negligible characteristics compared to the other system dynamics). Therefore, these elementary commands V are not discussed, in the following sections, contrary to the controlled Y, measured Z and control action U variables.
Controlled variables
Controlled variables are system variables to which targets are assigned. Control theory speaks of "tracking" when these targets are time dependent. Some authors use the term "regulation" in a general sense, for all types of targets (constant or variable), while others only in the case of a null constant target. In this article, the term "regulation" is used in a general sense and "tracking" to refer to the time dependent feature of the target.
Controlled variables on an irrigation canal can be of two types: flows (discharges) or efforts (water levels), according to the terminology used in physical system modelling through bond - graphs (Bond - graph is a method defined in the sixties and recently further developed, used for the representation and study of physical systems. Cf. Borne et al. 1992). They can equally be volumes, which means integral of flows (discharges) in reference to time, or integral of efforts (water levels) in reference to space.
Discharges
The needs of irrigation canal users are defined mainly in terms of discharge. For example, agricultural needs are expressed in terms of given discharges delivered to a plot, to a secondary canal, or to a pumping station, environmental needs as tailend discharge, or minimal discharge, urban needs as discharges delivered to a house or to a city water filtration plant, and industrial needs as discharges delivered to a factory. Natural or artificial storage reservoirs are sometimes available (e.g.: soil maximum water storage, lateral or on-line reservoir, basin of a water filtration plant, volume stored into the canal pools). Users' needs can then be defined in a more flexible way, in terms of volume distributed over a time period. In this case, the controlled variable is no longer a given value of discharge, but a volume, which is the integral of a discharge over a given time period. Discharge fluctuations are then authorised, and neutralised by the capacity of the storage reservoirs. However, these reservoirs are expensive and of limited sizes, and constraints of distribution never suppress needs expressed in terms of discharge.
Consequently, all free surface hydraulic system has to be managed, directly or indirectly, in order to satisfy users' demands in discharge. Considering the nature of the physical phenomenon at stake (gravity open channel flow from upstream to downstream), these demands in discharge can be satisfied only from the source situated at the upstream end of the system, by draining the upstream reservoirs. GPC (Sawadogo et al. 1991a, 1991b, 1992a, 1992b and 1992c, Rodellar et al. 1993), CACG (Piquereau et al. 1982 and 1984, Grosclaude et al. 1985, Verdier 1986, Tardieu 1988, Barbet 1990, Rey 1990, Trouvat 1991, Hurand et al. 1993), and SIMBAK (Chevereau 1991) are examples of regulation methods controlling discharges.
Water levels
Contrary to discharges, water levels can be easily measured in free surface canals and rivers. Furthermore, constraints of feeding gravity turnouts, stability of canal banks, efforts to reduce weed growth, constitution of intermediate water storage volumes, risks of overflow, are expressed in terms of water levels. Controlled water levels "y" can be upstream (yup, Figure 3), downstream (ydn, Figure 4), or intermediate inside the pool (yin, Figure 5). On Figures 3 and 4, controlled water level values are equal at null and maximum discharges. This is not always the case (e.g.: GEC Alsthom Gates). The corresponding water level difference is called "decrement". Operational characteristics are very different depending on the location of "y".

Fig. 3.

Fig. 4.
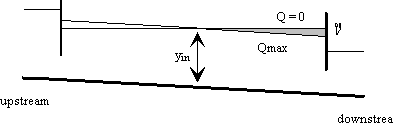
Fig. 5.
One of the advantages of controlling upstream water levels is that a storage volume V is available between the null discharge volume and the maximum discharge volume. It allows for rapid response to unforeseen demands of turnouts or downstream reaches and for storing water in case of a consumption reduction. But canal banks have to be horizontal, which is expensive. AVIS and AVIO gates (GEC Alsthom 1975-79 and 1981, Goussard 1993), and LittleMan downstream controller (developed by the USBR, Zimbelman 1987) are examples of such methods.
When downstream water levels are controlled, canal banks can follow the field natural slope, which reduces construction costs. But, no storage volume is available between the null discharge volume and the maximum discharge volume. Therefore, the system cannot response rapidly to unforeseen demands. The excess water cannot be stored locally and is "lost" in the downstream pools. AMIL gates (GEC Alsthom 1975-79 and 1981, Goussard 1993), ELFLO (Shand 1971, Buyalski et al. 1979), CARDD (Burt 1983), LittleMan upstream controller (Zimbelman 1987), PIR (Deltour 1992), PID (developed by UMA Engineering and applied at Imperial Valley, USA), PI (developed by Sogreah and applied at Kirkuk, Iraq), Zimbelman (developed by Zimbelman in 1981, Zimbelman 1987) are examples of downstream water levels control.
Controlling a particular intermediate water level, close to the middle of the pool, is equivalent to controlling the volume stored in the pool. This water level can be measured directly (no example has been found), or can be obtained as a linear combination of an upstream and a downstream water levels (e.g.: BIVAL). Controlling an intermediate water level is a compromise between the two previous options, in terms of construction cost and availability in storage volume V. Indeed, banks have to be horizontal only downstream of the controlled intermediate water level. But, one or several distant water levels have to be measured, which implies the installation of transmission lines or of a measurement network. BIVAL (developed by Sogreah, Zimbelman 1987, Chevereau 1991) is the only example of such a method.
Volumes
In this case, controllers are less sensitive to perturbations, but response times are increased (Framji et al. 1978). These methods are applicable to irrigation canals with important storage volumes, and equipped with turnouts whose feeding is not dependent on water levels in the main canal (e.g.: pumping stations). Dynamic Regulation (Coeuret 1977, Lefebvre 1977, Deltour 1988), and Controlled Volumes (Buyalski 1991) are examples of such methods.
Measured variables
Measured variables on irrigation canals are generally water levels (e.g.: ELFLO, PIR). In some cases, measured variables can be discharges (e.g.: CACG). A discharge can be measured with specific equipments (based in general on the measure of one or several flow velocities, with a propeller, an ultrasonic or electromagnetic device), through a cross structure equation Q (z1, z2, w), or a local control section rating curve Q (z) with a sufficient precision. When such an equation exists, it is assumed that a discharge Q is really measured, whatever the process used to obtain it, even if it is calculated from one or several water level measurements. A similar remark was made in Section 3. concerning water levels. Finally, measured variables can be volumes, evaluated by measuring several water levels along the canal, or by evaluating input - output discharge balance (e.g.: Dynamic Regulation).
Control action variables
Control action variables U are generally either gate openings, increments of gate opening, discharges, or increments of discharge. Gate openings has the advantage of taking into account the complex dynamics linking this opening with the local discharge and upstream and downstream water levels. These dynamics are important and it can be hazardous not to take them into account (e.g.: LQR CEMAGREF, ELFLO). Considering discharge as the control action variable allows for decoupling of the different subsystems. This is interesting when monovariable controllers are used in series (e.g.: Dynamic Regulation, PIR). However, the dynamics of the local controller linking the discharge (control action variable U) to the gate opening (elementary control action variable V) are not taken into account in the global controller. Therefore, the quality of the behaviour of the global controller cannot be assessed, since important dynamics are neglected in the design of the controller. If the control action variable U is a discharge, it is necessary to convert it into gate opening V, applicable to the system. This conversion can be done through the inversion of the device static equation Q (z1, z2, w), or by a local dynamic controller (e.g.: PID controller).
LOGICS OF CONTROL
Control engineers clearly define the logic of control concept depending on the type of information used to calculate the control action variables of the system. It can be "closed-loop", also called "feedback control" (FB), and "open-loop", also called "feedforward control" (FF).
Closed-loop control
In closed-loop, the control action variable U is calculated from the error measured between the real controlled variable Y and its corresponding target Yc (Figure 6). Perturbations P, even if unknown, are taken into account indirectly, through their effects on the output Y of the system. In control theory, this concept is essential since it links a control action variable U to a controlled variable Y. Closed-loops can be applied to all the controlled variables: discharge, water level and volume.
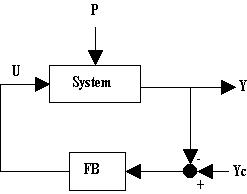
Fig. 6.
Examples of closed-loops in discharge are GPC (Sawadogo 1992a, Rodellar et al. 1993), CACG (Piquereau et al. 1982), CARA (Marzouki 1989, Roux 1992), and Liu et al. 1994.
Two types of closed-loops in water level are defined depending on the relative locations of the control action and controlled variable. Flows in irrigation canals are generally subcritical. Therefore, a water level can be controlled by modification of the upstream discharge, or by modification of the downstream water level (if the controlled water level belongs to the corresponding backwater curve). These modifications are made, respectively, from an upstream structure (Figure 7), or a downstream structure (Figure 8). Paradoxically, for technological historical reasons, the first logic of control is called feedback downstream control (FBdn), the second logic is called feedback upstream control (FBup).

Fig. 7.

Fig. 8.

Fig. 9.
Water level downstream control generates indirectly a discharge closed-loop control, since it is obtained from the modification of the upstream discharge. This characteristic is an essential property of the water level downstream control. Thanks to this remarkable particularity, a water level downstream control is sufficient, and no supplementary discharge control loop is necessary (neither in open-loop, nor in closed-loop). Examples of such methods are AVIS, AVIO gates, LittleMan downstream, ELFLO (Shand 1971), CARDD (Burt 1983), Zimbelman (1981), CARA (Marzouki 1989), BIVAL, PI developed by Sogreah, PID (Chevereau 1991), PIR (Deltour 1992), Liu et al. 1994.
Contrary to water level downstream control, water level upstream control does not generate any discharge control, since it is obtained by simple modification of the downstream water level. Therefore, a water level upstream control is not sufficient. It has to be completed by an explicit discharge control loop (in open-loop or in closed-loop). Examples of such methods are AMIL gate, LittleMan upstream, PID developed by UMA Engineering, and Duckbill weir. Even if this latter device is fixed, it can be considered as functioning in closed-loop since it maintains a quasi-constant water level whatever the perturbations acting on the system are.
Some water level control methods combine upstream and downstream control logics (Figure 9). They are called feedback mixed controls (FBmi). Since they also indirectly generate a closed-loop discharge control, they are often called, to simplify, downstream controls. Examples of such methods are LQR (Corriga et al. 1980, 1982a, 1982b and 1983, Balogun 1985 and 1988, Garcia 1988 and 1992, Hubbard et al. 1987, Reddy 1986, 1990, 1992a and 1992b, Filipovic et al. 1989, Florea et al., Malaterre 1994, Sawadogo et al. 1994), and Mixed gates (GEC Alsthom, used by the CNABRL). The latter are sometimes designated as "associated levels gates", because, in certain hydraulic conditions, the purpose of the gate is to maintain a constant difference between its upstream and downstream water levels. We consider this gate as a "mixed control" gate, because modification of a water level in a pool implies the combined reaction of the two gates located upstream and downstream of this water level.
In the case of a closed-loop in volume, system control structures are operated in function of errors between controlled volumes in various pools and the corresponding targeted volumes. In general, the volume of a pool is controlled through an upstream discharge modification. Therefore, the volume control generates implicitly a discharge control. Dynamic Regulation (SCP) and Controlled Volumes (USBR) are examples of such methods. Volumes could also be controlled through a downstream level modification.
For complex processes, like dead time processes (processes with time delays, Kuanyi 1989), closed-loops do not give entire satisfaction. In the case of irrigation canals, time delays between upstream control actions and downstream controlled variables are important (a few minutes to several hours). A single closed-loop can function correctly only if important storage volumes are available. Indeed, control delay is, at least, equal to the system delay. But storage volumes imply high construction costs. The quality of the control can be considerably improved by adding an open-loop (Shinskey 1988).
Open-loop control
In open-loop, the control action U is calculated knowing the dynamics of the system (using a model), the targeted output Yc and possibly an estimation of perturbations (Figure 10). The open-loop can compensate inherent system time delays by anticipating users' needs. These needs have to be estimated as precisely as possible. They should take into account climatic, agronomic, and sociological data, as well as recordings of the water consumption of previous weeks or seasons (Perrin 1989). An open-loop is generally insufficient, due to model errors, perturbation estimation errors, and unknown perturbations. Open-loops can be applied to all the controlled variables: discharge, water level and volume.

Fig. 10.
Examples of open-loops in discharge are given depending on the calculation method used:
- By model inversion: kinematic wave or pure delay (CARA, Roux 1992), diffusive wave (CACG, Sawadogo 1992a), dynamic wave (Chevereau 1991: SIMBAK, O'Laughlin 1972, Liu et al. 1992, USBR 1979 and Falvey 1987: Gate Stroking). These different methods are studied and compared by Chevereau (1991).
- By optimisation (Najim 1981, Sabet et al. 1985, Tomicic 1989, Khaladi 1992, Lin et al. 1992).
Example of open-loops in water level are:
- By inversion of the dynamic wave model (O'Laughlin 1972, Liu et al. 1992, USBR 1979, Falvey 1987).
- By optimisation (Tomicic 1989, Khaladi 1992, Lin 1992).
- By simulation (Malaterre 1989, Baume et al. 1993).
Some examples are quoted both in control of discharges and of water levels. For example, the dynamic wave model calculates simultaneously these two types of variables.
Sabet et al. (1985) is an example of an open-loop in volume.
Conclusion
Both closed-loops and open-loops have advantages and limitations. For these reasons, the combination of open-loop and closed-loop is often used (Figure 11), the closed-loop allowing to compensate the open-loop errors. For a multivariable system (with several control action and controlled variables), several controllers with different logics of control can be combined. For example, discharges can be controlled in open-loop and water levels in closed-loop. Therefore, some regulation methods appear in several categories.
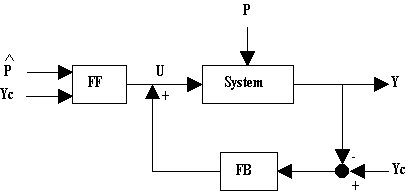
Fig. 11.
Water level downstream control and volume (downstream) control generate indirectly a discharge control. In the other cases (especially water level upstream control), two control loops are necessary. Usually, the discharge control is realised in open-loop and the water level control in closed-loop. This is due to the fact that contrary to discharges, water levels are easily measured (an open-loop uses estimates and a closed-loop uses measurements). Controlled variables must not be confused with logics of control, as some authors do. A water level controlled upstream of a structure (Figure 4) does not imply inevitably an upstream control (Figure 8), e.g.: ELFLO or PIR controllers. Furthermore, upstream control (Figure 8) is not synonymous of open-loop control (Figure 10), e.g.: AMIL gates.
METHODS OF DESIGN
Control theory implies a three steps process: the system modelling (i.e. the definition of a model), the system analysis (i.e. the study of the model behaviour), and the controller design (i.e. the determination of control action U leading to a desired dynamic behaviour of the controlled system, or the minimisation a criterion J). Following engineers' tools, methods of system analysis and controller design have evolved considerably. The first scientific calculation tools are more than three centuries old. Only very recently digital technology has revolutionised them. Currently, approximately 15 dynamic simulation tools are available on microcomputer. The 19th Annual Advanced Control Conference (August 1993), at the University of Purdue, was entirely devoted to these dynamic simulation tools (Kompass 1993). During the last twenty years, these improvements have allowed control theory research projects and applications to evolve from analog monovariable control to digital state space multivariable control.
Definition of inputs / outputs
Control action variables U and controlled variables Y of a given controlled system have been defined in Section 3. Variables U are particular inputs (respectively outputs) of the system (respectively of the controller). Since our classification concerns controllers and not systems we choose to define, in this article, "inputs" and "outputs" in reference to the controller and not to the system. The different types of inputs and outputs are illustrated in Figure 12, where:
U' are variables acting on the system, and not generated by the controller (e.g.: non controllable inputs, perturbations),
U'' variables generated by the controller, and not acting on the system (e.g.: control action variables for another system),
Y' variables generated by the system, and not directly used by the controller (e.g.: measured variables Z),
Y'' variables used by the controller, and not generated by the system (e.g.: measured variables Z, transfer of commands U coming from other controllers).

Fig. 12.
Inputs (respectively outputs) of the controller are therefore the above-mentioned variables Y and Y'' (respectively U and U'').
A monovariable controller (in input and output) has only one input and one output (variables being considered as scalars and not as vectors). Monovariable methods are also called SISO (Single Input, Single Output). A multivariable controller (in input and in output) considers several inputs and several outputs (scalars). Multivariable methods are also called MIMO (Multiple Inputs, Multiple Outputs). Controllers can be multivariable solely in inputs (MISO) or solely in outputs (SIMO). The numbers n of inputs and m of outputs of the controller can be indicated by qualifying the method of nI mO (e.g.: 3I 2O for CARDD method). Usually a method having a unique output is called monovariable, even if it has multiple inputs (nI 1O). Similarly, a method having several outputs (nI mO, m > 1) is called multivariable. This simplification is probably due to the fact that the theoretical and mathematical background of a control method is more linked to its number of outputs than to its number of inputs. This simplified terminology is used in the two following sections.
Dynamic Regulation, PIR and ELFLO + decouplers controllers use a control action variable U of adjacent upstream or downstream controllers. U is then considered as a supplementary input of the controller, but not as a supplementary output of the adjacent controllers (unless it is a specific output variable U'').
Monovariable methods
Heuristic monovariable methods have been developed based on hydraulics and not on control theory (e.g.: Zimbelman (1987), CARDD (Burt 1983)). Although quoted in the literature they are hardly operational and too site specific. An empirical method used by CARA on river-pond systems (Marzouki 1989) is being modernised (Roux 1992). LittleMan (USBR, Buyalski 1991) is an empirical method based on a three position controller.
Most of the irrigation canal control methods based on control theory use the well-known linear monovariable PID controller. This PID controller can be tuned with the Ziegler-Nichols method or by pole placement (Larminat 1993, Aström et al. 1993). Examples of PID related methods are:
P: AMIL, AVIS, AVIO,
PI: ELFLO, BIVAL, Dynamic Regulation, PI Sogreah,
PID: PID UMA Engineering.
Although very efficient in most cases, PID controllers do not explicitly take into account the characteristic canal time delays. Shand (1971) prospected the possibility to use a Smith Predictor in order to overcome this problem, when studying the automation of Corning Canal, California, USA. Developing an analog dead time model raised technological difficulties. Therefore, though less efficient, ELFLO method was eventually selected. Recently, the combination of a PI controller with a Smith Predictor was further developed (Deltour 1992, Sanfilippo 1993). This controller is called PIR. Modern digital technology has solved problems faced by Shand.
Other linear controllers have been used on river systems with long time delays by CACG. High order transfer functions are used, and tuned with the pole placement technique.
The generalised predictive control method (GPC), a monovariable optimisation method, has been developed by Sawadogo (1992) and Rodellar (1993). It is not based on the desired closed-loop behaviour, but on the minimisation of a criterion J, pondering the control action variable and the error between the controlled variable and its targeted value. GPC method uses transfer function models (Chan et al. 1990, Soeterboek 1990, Lee et al. 1990, Linkens et al. 1992). It naturally incorporates an open-loop and a closed-loop.
Methods based on fuzzy control (e.g.: CNABRL on the T2 canal, Marrakech, Morocco), expert systems, or neural networks (e.g.: Schaalje et al. 1993, Toudeft 1994) are being developed. These methods are still prospective, and should be tested.
Monovariable methods require to split the system into several subsystems without taking explicitly into account interactions between them. An irrigation canal is a multivariable system presenting strong interactions between subsystems. For example, the operation of a gate influences several upstream and downstream pools. The decoupler technique has been applied to ELFLO controller (Schuurmans 1992). It restrains, as far as possible, the influence of one control action on the unique regulator controlled output. The global multivariable process can then be considered as a series of independent monovariable non interactive processes evolving in parallel. This is possible if the number of inputs is superior or equal to the number of outputs (Borne et al. 1990). Performance of a controller can be greatly improved through decoupling. Decoupling requires a linear model of the system. Its performance is therefore decreased due to unknown perturbations and model errors. Although PIR (Deltour 1992), and Dynamic Regulation do not consider explicitly coupling effects, they attempt to reduce them. The discharge and not the gate opening is chosen as the control action variable, which is similar to decoupler II of Schuurmans (1992). Furthermore, part of the gate control action is transferred to the previous upstream controller, which is similar to decoupler I of Schuurmans (1992).
Multivariable methods
Control engineers have developed several multivariable methods. However, very few of them have been used on canals. For example, pole placement technique in state space, and multivariable PID have never been applied to irrigation canal regulation.
Different model inversion methods are described in the literature, leading generally to open-loop controllers (Chevereau 1991, Liu et al. 1992), and more rarely to closed-loop controllers (Liu et al. 1994).
Optimisation methods have also been developed. These methods are, in essence, multivariable. Different methods exist: linear optimisation (Sabet 1985), non-linear optimisation (Tomicic 1989, Khaladi 1992, Lin 1992), and LQR (Corriga 1983, Florea, Balogun 1985, Hubbard 1987, Garcia 1988, Filipovic 1989, Reddy 1992, Malaterre 1994, Sawadogo et al. 1994). The classical non-linear optimisation leads solely to an open-loop, sensitive to errors and perturbations. In order to introduce a closed-loop, the optimisation has to be processed periodically (for example at each time step). This complicates the method and limits its applications due to real-time constraints. Furthermore, the determination of real initial conditions, required for the optimisation, is not easy. On the other hand, LQR methods, based on a state space representation, incorporate, in essence, an open-loop and a closed-loop.
The implementation of multivariable methods is far more complex than for monovariable methods.
FIELD IMPLEMENTATION
This section presents different types of field implementation of canal regulation methods. Usual ones are described in the literature (Plusquellec 1988, Goussard 1993, Plusquellec et al. 1994, p. 36). They are briefly described hereafter.
Field implementation must not be confused with the design method. For example, a regulator based on a given design method (e.g.: a PI controller) can be locally controlled, i.e. one controller for each individual pool (e.g.: ELFLO), or distantly controlled, from a centralised control location (e.g.: Dynamic Regulation). Similarly, a given regulator can be manually operated on site (BIVAL at the Niger Office, Mali), or automatically controlled by a programmable logical controller (BIVAL, at the Rio Cupatitzio - Tepalcatepec, Mexico).
Different aspects of field implementation of regulation methods can be distinguished. They are the configuration (e.g.: localised, centralised), the devices (e.g.: weirs, manual gates, automatic gates), the instrumentation (e.g.: water level sensor, discharge measurement device), communications (e.g.: messenger, telephone line, radio-transmission), calculation and data processing (e.g.: empirical method, abacus, hydromechanical principle, calculator, microcomputer, workstation).
The following sections focus on the aspects of configuration and devices. The latter are the most important ones for the understanding of the characteristics of a canal regulation method, including its advantages, disadvantages, performance and constraints.
Configuration
Field implementation configuration concerns the spatial links between controllers, devices and controlled variables, and hierarchical links between controllers. It can be classified according to the following partition rule: local close, local distant, semi-local, centralised and hierarchised.
In local close configuration (Figure 13) each device is controlled by an independent controller, using only local information (measured variables), located close (around a few meters) to the device (e.g.: PID UMA Engineering, LittleMan, GEC Alsthom Gates).
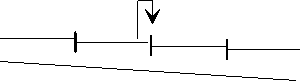
Fig. 13.

Fig. 14.

Fig. 15.
Local distant configurations (Figure 14) are similar to local close configurations, except that measured variables are distant from the device. For example, they can be located at the downstream end of the pool (e.g.: ELFLO, PIR, BIVAL, CARDD, Zimbelman).
In semi-local configuration (Figure 15) controllers are no longer independent. They explicitly use data generated by adjacent controllers. For example, a controller can use the control action variable of the next downstream controller (e.g.: PIR, ELFLO + decoupler).
In centralised configuration (Figure 16) all control actions are generated by a central controller (human being or computer), distant from the different devices. Control actions are gate openings (e.g.: Salt River Project), discharges, or water levels (e.g.: Central Arizona Project, Maricopa Stanfield Irrigation and District Drainage). Centralised control allows for supervision and remote control of the system. However, its implementation is more complex and more sensitive to hardware breakdowns than localised configurations.

Fig. 16.

Fig. 17.
In hierarchised configuration (Figure 17) control actions depend on different hierarchised decision-making levels. For example, automatic local distant controllers communicate with a centralised controller. This latter is in charge of target modifications and breakdown supervision.
The closed-loop component of Dynamic Regulation could be semi-local. However, the field implementation of this regulation method, at the Société du Canal de Provence, is centralised. This allows for combination of open-loop and closed-loop at the same control level, and for supervision of the system. A hierarchised control seems adapted to this type of regulation.
Devices
Different types of devices, used for field implementation of a given regulation method, can be classified according to the following partition rule: fixed device (e.g.: duckbill weir, proportional module), manual device, motorised device, mechanical automatic device (e.g.: AMIL, AVIS, AVIO gates), or electromechanical automatic device.
Mechanical automatic gates are relatively cheap, sufficiently precise and of easy maintenance. They are very well adapted to small or medium size canals. Electromechanical gates are even more precise and flexible. Target values and control algorithms can be easily modified, and remote control can be introduced. However, they are more expensive, less reliable, and more demanding in maintenance. Usually, they are used on large canals.
CONCLUSION
The first section showed how published classifications of canal regulation methods are insufficient. In order to fulfil this need, four essential characterisation criteria were defined: considered variables, logic of control, method of design and field implementation.
In Table 1, most of the published canal regulation methods are described, through this characterisation. However, some data are missing, due to the lack of clarity of the available literature. In addition to information relative to the four criteria, the developer name and examples of application or test are given. These methods are presented in alphabetical order of the name of the regulation method, so as not to favour one criteria.
Once this characterisation
is done, regulation methods can be classified easily, through the choice of a
classification criteria, and a partition rule (Table 2). For example,
regulation methods can be classified according to their logic of control. The
following partition rule, composed of two classes, can be defined: FF and FB. The
partition rule can be refined, if necessary, by subdividing these classes with
the FBup, FBmi and FBdn concepts. Another classification can be defined
according to the configuration of field implementation. The following partition
rule can then be defined: local close, local distant, semi-local, centralised,
and hierarchised.
Some regulation methods
include a single control loop (e.g.: AMIL gates). Their different
characteristics concern only this loop. In more complex cases, regulation
methods might include several control loops (e.g.: traditional local upstream
control, with one discharge open-loop, and several water level closed-loops). Their
regulation characteristics concern these different loops. Therefore, combined
information such as FF + FB or Q + y, appear in Table 1. This combined
information should also appear in Table 2 as classes of the partition rules. But,
in order to simplify the perusal of Table 2 they are not presented.
Such characterisations and
classifications are useful to get a better understanding of the features and
properties of each regulation method. Indeed, to each regulation characteristic
correspond directly advantages, disadvantages, performance and constraints. On
the other hand, such classifications allow for determination, for specific
features, of appropriate regulation methods.
Notes
1 Société du Canal de Provence
2 A pool is a portion of a
canal, situated between two control devices
3 Generalised Predictive
Control
4 United State Bureau of
Reclamation
5 Electronic Filter Level
Offset
6 Canal Automation for
Rapid Demand Deliveries
7 Proportionnel, Intégral, Retard
8 Proportional, Integral, Derivative
9 Linear Quadratic
Regulator, also called Optimal Control
10 Compagnie Nationale d'Aménagement du Bas-Rhône Languedoc
![]()
Pierre-Olivier Malaterre home page | CANARI server